题意:
给定一个字符串 s,计算 s 的 不同非空子序列 的个数。因为结果可能很大,所以返回答案需要对 10^9 + 7 取余 。
字符串的 子序列 是经由原字符串删除一些(也可能不删除)字符但不改变剩余字符相对位置的一个新字符串。
例如,”ace” 是 “abcde” 的一个子序列,但 “aec” 不是。
题目解析:
根据题意我们设dp[i]为前i个字符可以组成的不同的子序列,则有
dp[i] = dp[i – 1] + newCount – repeatCount
其中newCount为加上s[i]后新增的子序列个数,repeatCount为重复的子序列个数
于是我们只需要计算newCount和repeatCount即可
newCount的值比较好计算,就是dp[i – 1]。
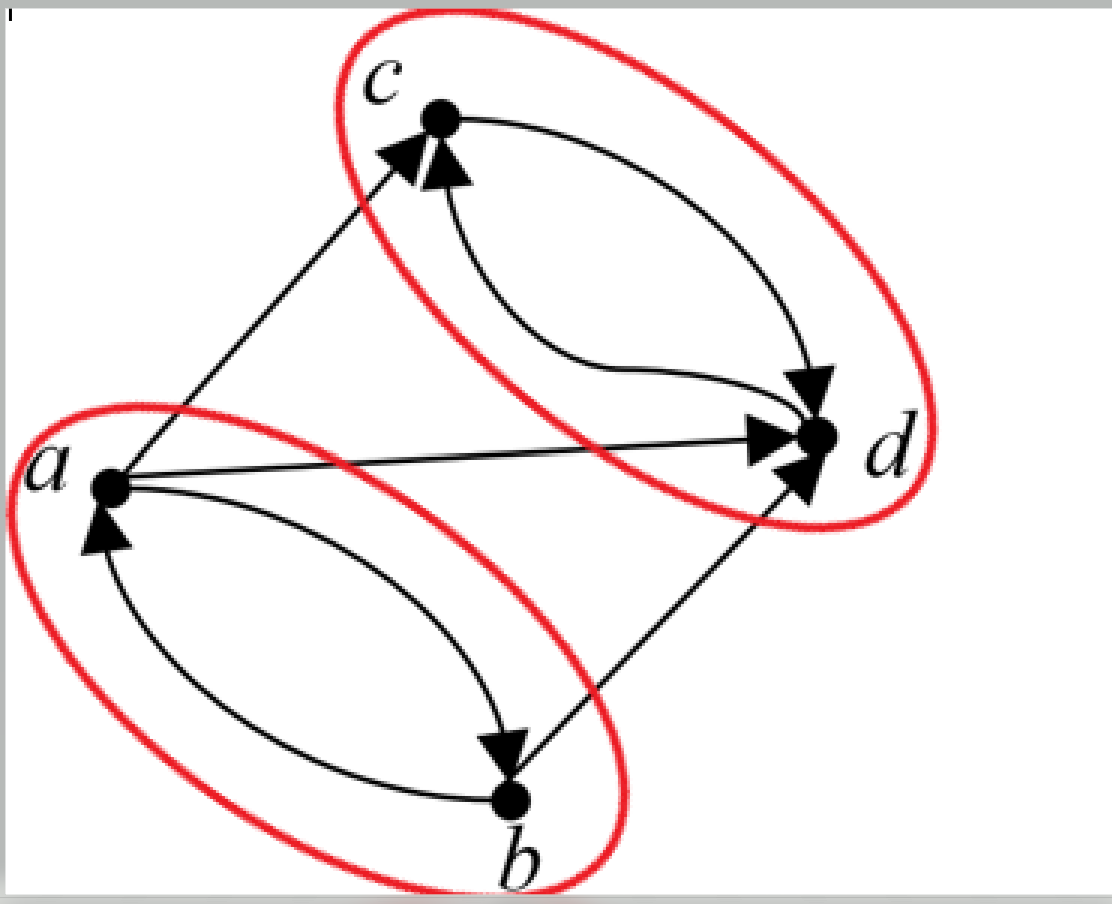
然后我们计算repeatCount,我们观察遍历到的第二个字符b,出现重复的序列为b和ab,而这两个序列正好是上一次添加b(也就是第②步)的时候新增的两个序列。于是我们可以使用数组preCount来记录上一次该字符新增的个数,该个数就是repeatCount。
由于dp[i]仅和dp[i-1]有关,我们可以滚动存储。
最后我们把空串减去即可。
![图片[1]-力扣每日一题-开心之家](https://pic.leetcode-cn.com/1665705779-Rterjh-image.png)
const int mod=1e9+7;
class Solution {
public:
int f[2222],c[33];
int distinctSubseqII(string s) {
int n=s.size();
s='q'+s;
f[0]=1;
for(int i=1;i<=n;i++ )
{
f[i]=(((f[i-1]*2-c[s[i]-'a'])%mod+mod))%mod;
c[s[i]-'a']=f[i-1];
c[s[i]-'a']%=mod;
}
return f[n]-1;
}
};
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END







- 最新
- 最热
只看作者