1.DFT:\(X(k) = \sum\limits_{n = 0}^{N - 1} {x(n){e^{ - j\frac{{2\pi }}{N}kn}}} ,k = 0,1,…,N - 1\)
2.欧拉公式:\({e^{jwn}} = \cos wn + j\sin wn\)
3.三角变换:\({sin{\rm{ }}\left( {{\rm{ }}2k\pi + a} \right){\rm{ }} = {\rm{ }}sina}\)
\(cos{\rm{ }}\left( {{\rm{ }}2k\pi + a} \right){\rm{ }} = cosa\)(k为整数)
4.IDFT反变换
\(x(n) = IDFT[X(k)] = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {X(k){e^{j\frac{{2\pi }}{N}kn}}} ,n = 0,1,…,N - 1\)
5.
\({\sum\limits_{n = 0}^{N - 1} {|x(n)|} ^2} = \frac{1}{N}{\sum\limits_{k = 0}^{N - 1} {|X(k)|} ^2}\)
6.DTFT定义:\(X({e^{j\omega }}) = \sum\limits_{n = - \infty }^\infty {x(n){e^{ - j\omega n}}} \)
1.求复指数序列x(u)=ejwn的共轭对称分量与共轭反对称分量。
![图片[1]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/11-1-1024x321.jpg)
2.求以下序列的共轭对称分量与共轭反对称分量。
\(x(u) = \{ 5,4 + j,2 - 6j,\underline 8 ,7 + j,6 - 3j,3 + j,2 \}\)
\(x(u) = \{ 5,4 + j,2 - 6j,\underline 8 ,7 + j,6 - 3j,3 + j,2 \}\)
注意答案6-2j变成6-3j,看下方法就行。
![图片[2]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/22-1024x357.jpg)
3.设x(n)为N=6点的实有限长序列
\(x(n) = \{ \underline 1 ,2,4,3,0,5\}\)
试确定以下表达式的数值,并用MATLAB计算DFT进行验证。
(1)X(0) (2)X(3) (3)\(\sum\limits_{k = 0}^5 {X(k)} \) (4)\(\sum\limits_{k = 0}^5 {|X(k)} {|^2} \)
\(x(n) = \{ \underline 1 ,2,4,3,0,5\}\)
试确定以下表达式的数值,并用MATLAB计算DFT进行验证。
(1)X(0) (2)X(3) (3)\(\sum\limits_{k = 0}^5 {X(k)} \) (4)\(\sum\limits_{k = 0}^5 {|X(k)} {|^2} \)
![图片[3]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/31-1024x636.jpg)
![图片[4]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/311-1024x477.jpg)
MATLAB程序
n=1:6;
xn=[1,2,4,3,0,5];
N=length(n);
[Xk]=fft(xn,N);
y1=Xk(1)
y2=Xk(4)
y3=sum(Xk)
y4=sum(abs(Xk).^2)4.已知x(n)如图 P3.4所示为\(\{ \underline 1 ,1,3,2\} \),试画出\(x{(( - n))_5},x{(( - n))_6}{R_6}(n),x{((n))_3}{R_3}(n),x{((n))_6},x{((n - 3))_5}{R_5}(n),x{((n))_7}{R_7}(n)\)等各序列。
![图片[5]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/3.4.png)
![图片[5]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/3.4.png)
补0翻转,移位补0。
![图片[6]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/4-1024x885.jpg)
5.已知\(x(n) =\{ \underline 2 ,1,4,2,3\} \)
(1)计算\(X({e^{j\omega }}) = DTFT[x(n)]\)及\(X(k) = DFT[x(n)]\),并说明二者的关系。
(2)将x(n)的尾部补零,得到\({x_0}(n) = \{ \underline 2 ,1,4,2,3,0,0,0\} \)
计算\({X_0}({e^{j\omega }}) = DTFT[{x_0}(n)]\),\({X_0}(k) = DFT[{x_0}(n)]\)
(3)将(1)、(2)的结果加以比较,得出相应的结论。
(1)计算\(X({e^{j\omega }}) = DTFT[x(n)]\)及\(X(k) = DFT[x(n)]\),并说明二者的关系。
(2)将x(n)的尾部补零,得到\({x_0}(n) = \{ \underline 2 ,1,4,2,3,0,0,0\} \)
计算\({X_0}({e^{j\omega }}) = DTFT[{x_0}(n)]\),\({X_0}(k) = DFT[{x_0}(n)]\)
(3)将(1)、(2)的结果加以比较,得出相应的结论。
![图片[7]-数字信号DFT课后习题-开心之家](https://hpa888.top/wp-content/uploads/2022/10/5-1024x590.jpg)
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END




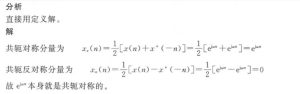



暂无评论内容