图的矩阵表示做题总结

离散书上清晰的讲解了无向图的关联矩阵（p161），无书的同学可看下图，我就不做讲解。

我们主要谈谈有向图的关联矩阵，在有向图D=<V，E>中，e_j离开v_i（箭头指出），则m_ij=1；e_j进入v_i（箭头指入），则m_ij=-1；e_j和v_i不相关联，则m_ij=0.

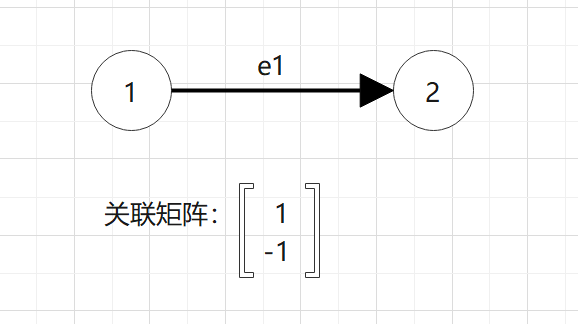
例1：在图D中，e₁为<v₁,v₂>,关联矩阵表示如下图。（画图太烂了，大家将就看一下，难搞哦）

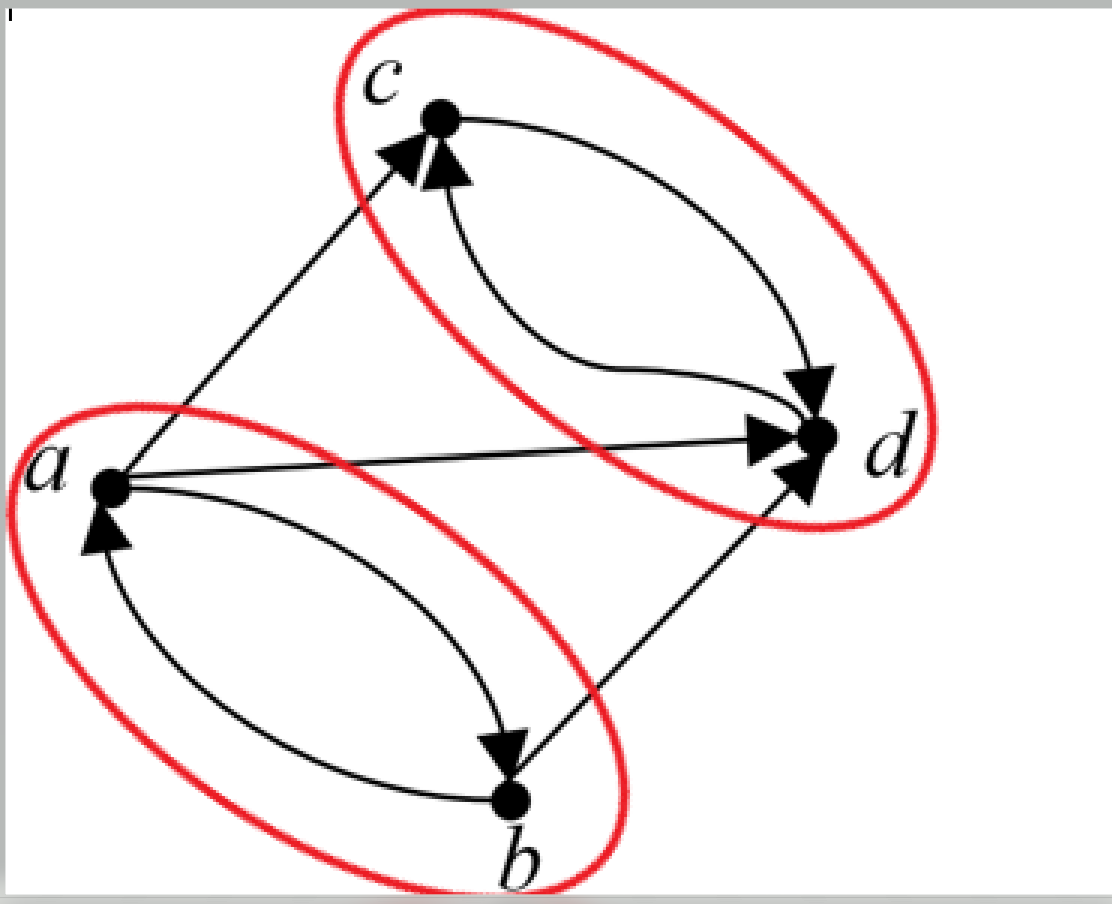
例2：学习通上的题，这个好看多了。

A=[0,1,0,1;1,0,1,1;0,1,1,0;1,1,0,0]; %输入邻接矩阵
I=eye(4); %4阶单位矩阵（可变，随矩阵A的阶数改变）
S=A+I; %A⁰+A¹
p=S;
for i=2:4 %4为邻接矩阵A的阶数（随矩阵A的阶数改变）
p=p+A^i; %A²+A³+A⁴（一直加到Aⁿ，n为矩阵A的阶数）
end
p(p~=0) =1; % 将不为0 的元素变为1
p

设A为p阶图G=<V，E>的邻接矩阵，其中V={v₁，v₂，···，v_p}。

v_i到v_j长度为n的通路数：矩阵A的n次幂Aⁿ（n=1，2，3，···）中的元素a_ij^（n）表示v_i到v_j长度为n的基本通路的总数。

长度为n的通路总数：矩阵中元素a_ij^（n）之和。

v_i到v_i长度为n的回路数：元素a_ii^（n）表示通过vi的长度为n的基本回路的总数。

长度为n的回路总数：矩阵主对角线之和。

设A为p阶图G=<V，E>的邻接矩阵。

1.找出图G的邻接矩阵A。

2.计算A的幂和C_A。（C_A=A⁰+A¹+···+A^p）

3.得出可达矩阵。（矩阵C_A中对应元素不为0标1，为0标0）

4.写出可达矩阵的转置矩阵。

5.分别求可达矩阵与它的转置矩阵的析取（求单向连通分图）和合取（求强联通分图）。