力扣每日一题

769. 最多能完成排序的块 – 力扣（LeetCode）

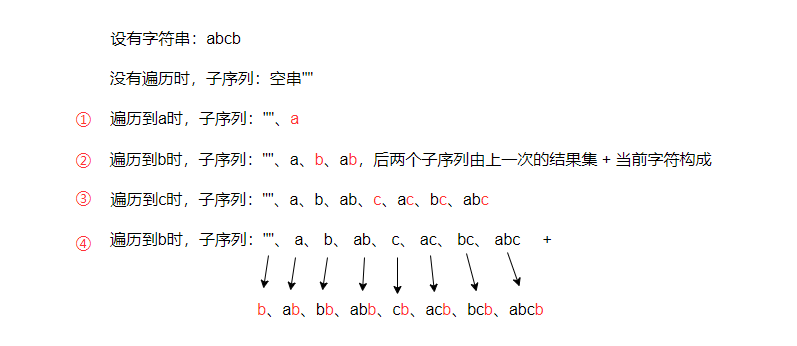
题意：给定一个长度为 n 的整数数组 arr ，它表示在 [0, n – 1] 范围内的整数的排列。

我们将 arr 分割成若干 块 (即分区)，并对每个块单独排序。将它们连接起来后，使得连接的结果和按升序排序后的原数组相同。

返回数组能分成的最多块数量。

解题思路：

根据题意我们可以得到以下两个定理：

定理一：对于某个块 A，它由块 B 和块 C 组成，即 A = B + C。如果块 B 和块 C 分别排序后都与原数组排序后的结果一致，那么块 A 排序后与原数组排序后的结果一致。
证明：因为块 B 和块 C 分别排序后都与原数组排序后的结果一致，所以块 B 的元素和块 C 的元素的并集为原数组排序后在对应区间的所有元素。而 A=B+C，因此将块 A 排序后与原数组排序后的结果一致。

定理二：对于某个块 A，它由块 B 和块 C 组成，即 A = B + C。如果块 A 和块 B 分别排序后都与原数组排序后的结果一致，那么块 C 排序后与原数组排序后的结果一致。
证明：如果块 C 排序后与原数组排序后的结果不一致，那么块 B 的元素和块 C 的元素的并集不等同于原数组排序后在对应区间的所有元素。而块 A 排序后与原数组排序后的结果一致，说明块 A 的元素等同于原数组排序后在对应区间的所有元素。这与块 A 的元素由块 B 的元素和 块 C 的元素组成矛盾，因此块 C 排序后与原数组排序后的结果一致。

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        int m = 0, res = 0;
        for (int i = 0; i < arr.size(); i++) {
            m = max(m, arr[i]);
            if (m == i) {
                res++;
            }
        }
        return res;
    }
};